Principles of Biochemistry 17 |ATP Synthesis| Class Notes |HarvardX

Quick View

$NADH + H^ + frac{1}{2}O_ 2 \to NAD^ + H_ 2O$

1. $NAD^ + + H^ + 2e^ - \to NADH$	E’O2~~ = - 0.32V
2. $ frac{1}{2}O_ 2 + 2H^ + + 2e^ - \to H_ 2O$	E’O1~~ = + 0.82V

$\Delta G’^ {\circ} = -nF\Delta E’^ {\circ} $
$n = 2$
$F = 96.5kJ/Vmol$
$\Delta　E’^ {\circ} = E’^ {\circ}_ acceptor - E’^ {\circ} _ donor $
$\ \ \ \ \ \ \ \ =0.82 -(-0.32)$
$\ \ \ \ \ \ \ \ =1.114 V$

$\Delta G’^ {\circ} = -220.1kJ/mol$

The movement of the proton:

$NADH + 11H^ +_ M + frac{1}{2}O_ 2 \to NAD^ + 10H^ +_ I +H_ 2O$

Energetic of a proton Gradient:
$\Delta = RT\ ln(frac{C_ I}{C_ M})+ ZF\Delta \Psi$
Chemical Potential + Electrical Potential

Derivation

In a simple reaction: S -> P
$\Delta G = \Delta G’^ {\circ} + RT\ ln[P]/[S]$

But in Transport across a membrane, there are no covalent bonds formed. As a result, the $\Delta G’^ {\circ} = 0$

$\Delta G = RT\ ln \frac{C_ I}{C_ M}$

$ln(C_ I/ C_ M) = 2.3log(C_ I / C_ M)$
$\ \ \ \ \ \ \ \ \ \ = 2.3(log(C_ I) - log(C_ M))$
$\ \ \ \ \ \ \ \ \ \ = 2.3(log[H^ +]_ I - log[H^ +]_ M)$

$pH = 1 / log[H^ +]= - log[H^ +]$
$ln(C_ I/ C_ M) = 2.3(pH_ M - pH_ I)$
$ln(C_ I/ C_ M) = 2.3 \Delta pH$
$$
\Delta G = 2.3 RT \Delta pH + F\Delta \Psi (when Z =1)
$$

• Experimental value:
  $\Delta \Psi = 0.15 - 0.2 V$

• Matrix pH > IMS pH
  $\Delta pH = +0.75$

• Energy cost to pump H+
  $\Delta G = 2.3 RT \Delta pH + F\Delta \Psi = 20kJ/mol H^ +$

• Energy cost to pump 10 moles H^+
  $\Delta G = 200 kJ/mol$

• The energy released by the transport of electrons through ETC:
  $220 kJ/mol$ of NADH oxidized,
  which is enough for pump 10 protons.

ATP Synthase

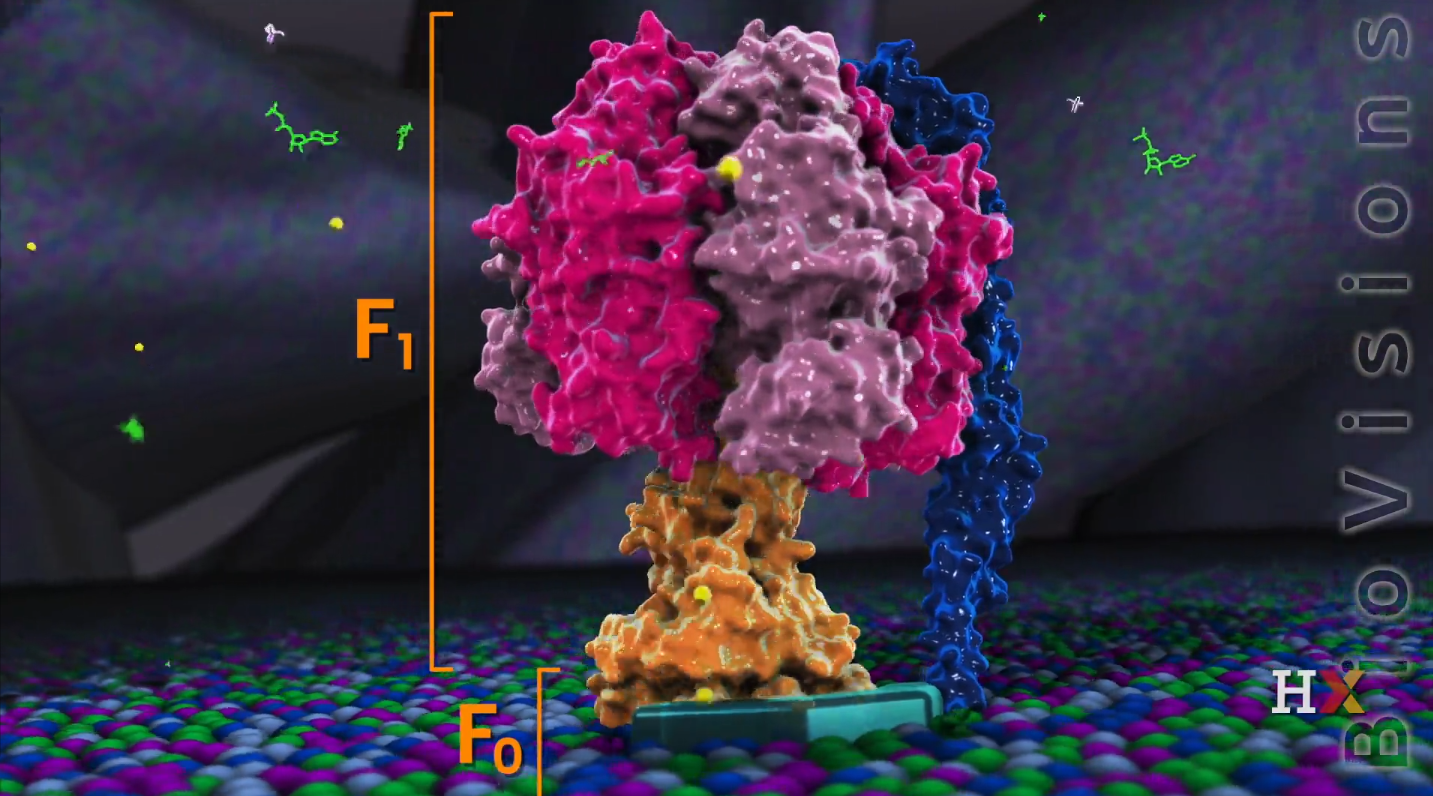
• It’s huge: over half of megadalton
• Like a motor
• Two main parts:
  1. F₀ sub-unit: one driven by protons
  2. F₁ sub-unit: one driven by ATP
• The ATP hydrolysis decrease the ATP, the proton pump drives the reverse action of ATP hydrolysis.

F₀ sub-unit

It contains 10 to 15 c-chains and each c-chain is composed of two alpha-helices scanning.
On the one side of the c-chain, there is a-chain that contains a proton channel and isolates a couple of c-chains from surround lipids.

F₁ sub-unit

It is an ATP driving motor that contains five types of chains:

• $\gamma$ and $\epsilon$ chains from the axle (the center) are also called a stalk. The stalk interact with the c-ring of the F₀ sub-units, and rotate through a ring of six chains: 3 $\alpha$ and 3 $\beta$ chains that from the rest of the F₁ subunit
• $\delta$ anchors the hexamer to the B subunit that embed into membrane and prevent itself rotating.
• 3 pair of $\alpha$ and $\beta$ dimmer in the bottom of the ATP synthase and form the core of this enzyme.
  • both of them could bind ATP.
  • $\alpha$ chain might have a catalytic regulatory role
  • $\beta$ chain has only catalytic role

The stalk is not symmetrical and forces the $\beta$ chains into 3 distinct conformations.

Binding Change Model

Paul Boyer.

$\beta$ Chains have three distinct states on ATP synthase:

• O state: open state, low affinity to ATP and ADP
  which means ATP and ADP could bind and lose easily.
• L state: loss conformation. it has a high affinity to ADP and inorganic phosphate.
• T state: tight conformation which is the high avidity for ATP

Each $\beta$ chain was bound with a molecule of ATP. As a result, three ATP are produced per turn of the stalk.

Protons Caclultion

There is 10 to 15 (#N) number of c-chains in a ring. So, it needs #N protons. to flow back to through F₀. A full turn of c-chain also corresponded with producing 3 APT molecules. Therefore, the proton need for each ATP is #N/3

proton motive force

• ATP is used outside of mitochondria.
  • Adenine translocase coordinates the ATP-ADP exchange.
  • ATP carries 4 negative charges,
  • ADP carries 3 negative charges.
  • ATP transport causing one negative charge into the interspace.
• phosphate
  • Phosphate translocase is responsible for the transport of PO₄^-
  • It’s neutralized the charge brings by ATP transport.