Python: Find the outline (edge) of the 2D points

Python: Find the outline (edge) of the 2D points

This passage is for showing how to find the boundary of a group of the point. One major problem of boundary searching is the groove. I rigid groove threshold may cut the points into two or more groups. For the flexibility of the script, the perimeter alpha was set for determining the threshold of the boundary. The larger alpha value, the more tolerance for the grooves.

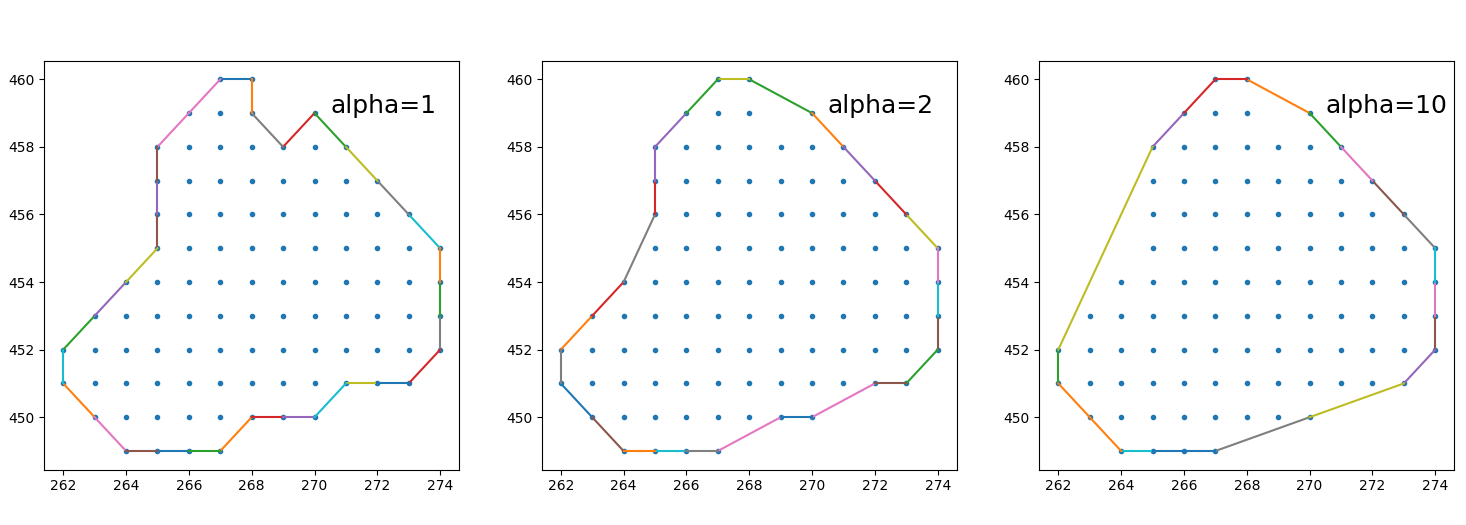
from scipy.spatial import Delaunay
import numpy as np

points = np.array([[262, 451], [262, 452], [263, 450], [263, 451], [263, 452], [263, 453], [264, 449], [264, 450], [264, 451], [264, 452], [264, 453], [264, 454], [265, 449], [265, 450], [265, 451], [265, 452], [265, 453], [265, 454], [265, 455], [265, 456], [265, 457], [265, 458], [266, 449], [266, 450], [266, 451], [266, 452], [266, 453], [266, 454], [266, 455], [266, 456], [266, 457], [266, 458], [266, 459], [267, 449], [267, 450], [267, 451], [267, 452], [267, 453], [267, 454], [267, 455], [267, 456], [267, 457], [267, 458], [267, 459], [267, 460], [268, 450], [268, 451], [268, 452], [268, 453], [268, 454], [268, 455], [268, 456], [268, 457], [268, 458], [268, 459], [268, 460], [269, 450], [269, 451], [269, 452], [269, 453], [269, 454], [269, 455], [269, 456], [269, 457], [269, 458], [270, 450], [270, 451], [270, 452], [270, 453], [270, 454], [270, 455], [270, 456], [270, 457], [270, 458], [270, 459], [271, 451], [271, 452], [271, 453], [271, 454], [271, 455], [271, 456], [271, 457], [271, 458], [272, 451], [272, 452], [272, 453], [272, 454], [272, 455], [272, 456], [272, 457], [273, 451], [273, 452], [273, 453], [273, 454], [273, 455], [273, 456], [274, 452], [274, 453], [274, 454], [274, 455]])

Functions: Iddo Hanniel; 2018

def alpha_shape(points, alpha, only_outer=True):
    """
    Compute the alpha shape (concave hull) of a set of points.
    :param points: np.array of shape (n,2) points.
    :param alpha: alpha value.
    :param only_outer: boolean value to specify if we keep only the outer border
    or also inner edges.
    :return: set of (i,j) pairs representing edges of the alpha-shape. (i,j) are
    the indices in the points array.
    """
    assert points.shape[0] > 3, "Need at least four points"
    def add_edge(edges, i, j):
        """
        Add an edge between the i-th and j-th points,
        if not in the list already
        """
        if (i, j) in edges or (j, i) in edges:
            # already added
            assert (j, i) in edges, "Can't go twice over same directed edge right?"
            if only_outer:
                # if both neighboring triangles are in shape, it's not a boundary edge
                edges.remove((j, i))
            return
        edges.add((i, j))
    tri = Delaunay(points)
    edges = set()
    # Loop over triangles:
    # ia, ib, ic = indices of corner points of the triangle
    for ia, ib, ic in tri.vertices:
        pa = points[ia]
        pb = points[ib]
        pc = points[ic]
        # Computing radius of triangle circumcircle
        # www.mathalino.com/reviewer/derivation-of-formulas/derivation-of-formula-for-radius-of-circumcircle
        a = np.sqrt((pa[0] - pb[0]) ** 2 + (pa[1] - pb[1]) ** 2)
        b = np.sqrt((pb[0] - pc[0]) ** 2 + (pb[1] - pc[1]) ** 2)
        c = np.sqrt((pc[0] - pa[0]) ** 2 + (pc[1] - pa[1]) ** 2)
        s = (a + b + c) / 2.0
        area = np.sqrt(s * (s - a) * (s - b) * (s - c))
        circum_r = a * b * c / (4.0 * area)
        if circum_r < alpha:
            add_edge(edges, ia, ib)
            add_edge(edges, ib, ic)
            add_edge(edges, ic, ia)
    return edges

Usage:

import matplotlib.pyplot as plt
# Plotting the output
fig, ax = plt.subplots(figsize=(18,4))

edges = alpha_shape(points, alpha=1, only_outer=True)
plt.subplot(1, 3, 1)
plt.plot(points[:, 0], points[:, 1], '.')
for i, j in edges:
    plt.plot(points[[i, j], 0], points[[i, j], 1])

plt.text(270.5,459, "alpha=1", size=18)


edges = alpha_shape(points, alpha=2, only_outer=True)
plt.subplot(1, 3, 2)
plt.plot(points[:, 0], points[:, 1], '.')
for i, j in edges:
    plt.plot(points[[i, j], 0], points[[i, j], 1])

plt.text(270.5,459, "alpha=2", size=18)

edges = alpha_shape(points, alpha=10, only_outer=True)
plt.subplot(1, 3, 3)
plt.plot(points[:, 0], points[:, 1], '.')
for i, j in edges:
    plt.plot(points[[i, j], 0], points[[i, j], 1])

plt.text(270.5,459, "alpha=10", size=18)
plt.show()