Multi-layer Neural Nets
From linear to nonlinear classifiers
- Linear classifier
- a linear classifier computes $f(x) = argmax\ Wx$
- The resulting classifier divides the x-space into Voronoi regions: convex regions with piece-wise linear boundaries
- Nonlinear classifier
- Not all classification problems have convex decision regions with PWL boundaries!
- Here’s an example problem in which class 0 (blue) includes values of x near [0.8,0]T, but it also includes some values of x near [0.4,0.9]T
- You can’t compute this function using: $f(x) = argmax\ Wx$
- The solution: Piece-wise linear functions
- Nonlinear classifiers, can be learned using piece-wise linear classification boundaries
- Nonlinear regression problems, can be learned using piece-wise linear regression
- In the limit, as the number of pieces goes to infinity, the approximation approaches the desired solution
Introduction
Video tutorial: Intro to Deep Learning; Apr. 29, 2024
Slides PDF: Slides
Perceptron and Neural Network
For multi Output Perceptron:
| Multi Output Perceptron | Single Layer Neural Network |
|---|---|
 |
 |
| $$z_i = w_{0,i} + \sum^m_{j=1} x_j w_{j,i}$$ | $$ z_i = w_{0,i}^{(1)} + \sum_{j=1}^{m} x_j w_{j,i}^{(1)} $$ $$ \hat{y}_ i = g \left( w_ {0,i}^ {(2)} + \sum_ {j=1}^ {d_ 1} g(z_ j) w_ {j,i}^ {(2)} \right) $$ |
| © Alexander Amini | © Alexander Amini |
By comparing them based on this illustration, we can see that the Perceptron and neural network architectures are very similar. The difference lies in the output parts. For a Perceptron, after the perceptron learns the $z$, the results are based directly on $g(z)$. However, in a neural network, after the model learns $z$, it still needs to learn the $w^{(2)}$, and the result is based on both $z$ and $w^{(2)}$. In this case, $z$ becomes a hidden layer.
For Deep neural network, we just simply increasing the layers of hidden layer which is $z_ n → z_ {n, m}$.
Quantifying Loss
By following the function above, we know that for a single layer neural net work with single output, $\hat{y} = g \left( w^ {(2)} + \sum_ {j=1}^ {d_ 1} g(z_ j) w_ {j}^ {(2)} \right) $ or just $\hat{y} = g(x^{(i)}; W)$. So, we could define that the loss: $\mathcal{L}(f(x^{(i)}; \mathbf{W}), y^{(i)})$. Hence, the Empirical Loss which measure the total loss should be:
$$
J(W) = \frac{1}{n} \sum^n_ {i=1} \mathcal{L}(f(x^{(i)}; \mathbf{W}), y^{(i)})
$$
According to the classification test or regression test, we could selected tow types of basic loss function:
Binary Cross-Entropy Loss:
- $ \mathcal{L} = -\frac{1}{N} \sum_{i=1}^{N} \left[ y^{(i)} \log(f(x^{(i)})) + (1 - y^{(i)}) \log(1 - f(x^{(i)})) \right] $
Mean Squared Error Loss:
- $ \mathcal{L} = \frac{1}{N} \sum_{i=1}^{N} \left( y^{(i)} - f(x^{(i)}) \right)^2 $
Training
The logic of training is very simple and clear: we want to find the weight that achieve the lowest loss.
We random pick initial value of $w$ and updated when we find a new $w$ which could achieve lower loss. By doing this, we could compute the gradient: $ \frac{\partial J(W)}{\partial W} $
The way of update the weight is very similar to perceptron:
- $W \leftarrow W - \eta \frac{\partial J(w)}{\partial w} $
Backpropagation
Backpropagation is a key algorithm in training neural networks, which utilizes the chain rule to compute the gradient of the loss function with respect to each weight in the network. Let’s break down the images and the concepts step-by-step:
Backpropagation, short for “backward propagation of errors,” is a fundamental algorithm used to train artificial neural networks. It is based on the concept of gradient descent and helps in minimizing the error by adjusting the weights of the network. Here’s a step-by-step explanation and a guide on how to calculate it:
Understanding Backpropagation
-
Forward Pass:
- Input data is passed through the neural network layer by layer to obtain the output.
- Each layer performs a weighted sum of inputs, applies an activation function, and passes the result to the next layer.
-
Loss Calculation:
- The network’s output is compared to the actual target output using a loss function (e.g., Mean Squared Error, Cross-Entropy Loss).
- The difference between the predicted output and the actual output is the error.
-
Backward Pass (Backpropagation):
- The error is propagated back through the network to update the weights.
- This involves computing the gradient of the loss function with respect to each weight in the network.
- Gradients indicate the direction and magnitude of the change required in the weights to minimize the error.
Steps in Backpropagation
-
Initialization:
- Initialize the weights and biases of the network with small random values.
-
Forward Pass:
- For each layer $ l $, compute the input $ z^l $ and output $ a^l $:
- $z^l = W^l a^{l-1} + b^l$
- $a^l = \sigma(z^l)$
- Here, $ W^l $ are the weights, $ b^l $ are the biases, $ \sigma $ is the activation function, and $ a^{l-1} $ is the output from the previous layer (the first $a$ is $x$ which is the input).
- For each layer $ l $, compute the input $ z^l $ and output $ a^l $:
-
Compute Loss:
- Compute the loss $ L $ using a suitable loss function.
-
Backward Pass:
- Calculate the gradient of the loss with respect to the output of the last layer $ \delta^L $:
- $\delta^L = \nabla_a L \cdot \sigma’(z^L)$
- For each layer $ l $ from $ L-1 $ to 1, compute:
-$\delta^l = (\delta^{l+1} \cdot W^{l+1}) \cdot \sigma’(z^l)$ - Update the weights and biases:
- $W^l = W^l - \eta \cdot \delta^l \cdot (a^{l-1}) ^T$
- $b^l = b^l - \eta \cdot \delta^l$
- Here, $ \eta $ is the learning rate, and $ \sigma’ $ is the derivative of the activation function.
- Calculate the gradient of the loss with respect to the output of the last layer $ \delta^L $:
Calculation
To actually calculate backpropagation, you need to:
- Initialize weights and biases.
- Perform a forward pass to compute the activations for each layer.
- Compute the loss using the output from the forward pass and the actual target values.
- Perform a backward pass to compute the gradients of the loss with respect to each weight.
- Update the weights and biases using the computed gradients and the learning rate.
Example Code (Python):
|
This code demonstrates the basic steps of backpropagation in a simple neural network. By running this code, you can observe how the network learns to approximate the XOR function over time.
In a perceptron, weights and biases are updated by multiplying the error (loss) by the input and learning rate, and then adding this value to the current weights. This approach works because the weights for each input are independent, and the perceptron does not form a network. However, in a neural network, nearly every weight can influence every output. As a result, we cannot simply update the weights based on the error alone. Instead, we need to calculate the contribution of each weight to the overall error and adjust the weights accordingly. This process of calculating each weight’s contribution and updating them is known as backpropagation.
Overview of the Process
- Forward Pass: The input $ x $ is passed through the network to compute the output $ \hat{y} $.
- Loss Calculation: The loss function $ J(W) $ calculates the difference between the predicted output $ \hat{y} $ and the actual output.
- Backward Pass: Gradients are computed by propagating the error backward through the network, adjusting the weights to minimize the loss.
The goal is to understand how a small change in one weight (e.g., $ w_2 $) affects the final loss $ J(W) $.
For the weight $ w_1 $, the gradient involves additional intermediate steps. Specifically:
$ \frac{\partial J(W)}{\partial w_1} = \frac{\partial J(W)}{\partial \hat{y}} \times \frac{\partial \hat{y}}{\partial z_1} \times \frac{\partial z_1}{\partial w_1} $
This decomposition shows that the gradient of the loss with respect to $ w_1 $ depends on:
- The gradient of the loss with respect to the output $ \hat{y} $
- The gradient of $ \hat{y} $ with respect to the intermediate variable $ z_1 $
- The gradient of $ z_1 $ with respect to the weight $ w_1 $
Why Backpropagation?
Backpropagation efficiently computes these gradients using the chain rule. The key points are:
- Efficiency: By reusing intermediate results (e.g., the gradient of the loss with respect to $ \hat{y} $), backpropagation avoids redundant calculations.
- Modularity: Gradients are computed layer by layer, allowing for modular network designs where each layer can be independently understood and modified.
- Training: These gradients are used to update the weights in a way that minimizes the loss function, allowing the network to learn from data.
Summary
Backpropagation applies the chain rule to compute gradients of the loss function with respect to each weight in the network. These gradients are essential for updating the weights during training, thereby enabling the network to learn. Understanding the chain rule and how it applies to neural networks is crucial for grasping backpropagation.
Batches
Running backpropagation can be computationally expensive when calculating (\frac{\partial J(W)}{\partial w_1}) with a large training dataset. It is easy to run out of memory if too many threads are used. To mitigate this, one approach is to use a single data point to compute (\frac{\partial J_i(W)}{\partial w_1}), though this can introduce significant noise. A more effective strategy is to divide the training data into small batches, which can increase training efficiency and reduce noise. Common batch sizes used during training are 32 or 64.
Strategies for Avoiding Overfitting
- Dropout:
- randomly set some activate as 0.
- force network not relay on any node
- Early stopping:
- monitor the losing curve and stop the training before it had change to overfit
NW in Action
Let’s go through an example of using TensorFlow to build a two-layer neural network for a classification task using a dataset from scikit-learn. We will use the Iris dataset, which is a classic dataset for classification.
Notice: When TensorFlow runs a neural network, it automatically detects and utilizes available GPUs to accelerate the computation. This process is seamless and doesn’t typically require manual intervention.
|
Epoch 96/100 4/4 [==============================] - 0s 3ms/step - loss: 0.2099 - accuracy: 0.9532 - val_loss: 0.3162 - val_accuracy: 0.9167 Epoch 96, Loss: 0.21823757886886597, Accuracy: 0.9351851940155029 Epoch 97/100 4/4 [==============================] - 0s 3ms/step - loss: 0.2010 - accuracy: 0.9522 - val_loss: 0.3123 - val_accuracy: 0.9167 Epoch 97, Loss: 0.21543042361736298, Accuracy: 0.9351851940155029 Epoch 98/100 4/4 [==============================] - 0s 3ms/step - loss: 0.2175 - accuracy: 0.9366 - val_loss: 0.3079 - val_accuracy: 0.9167 Epoch 98, Loss: 0.21266280114650726, Accuracy: 0.9351851940155029 Epoch 99/100 4/4 [==============================] - 0s 3ms/step - loss: 0.2047 - accuracy: 0.9428 - val_loss: 0.3040 - val_accuracy: 0.9167 Epoch 99, Loss: 0.20983757078647614, Accuracy: 0.9351851940155029 Epoch 100/100 4/4 [==============================] - 0s 3ms/step - loss: 0.2070 - accuracy: 0.9376 - val_loss: 0.3008 - val_accuracy: 0.9167 Epoch 100, Loss: 0.20734088122844696, Accuracy: 0.9351851940155029
 |
In this group of test data, there are ony one mistake. |
Another regression example write by torch
|
Limitations of Neural Networks
Failure in Sine Function

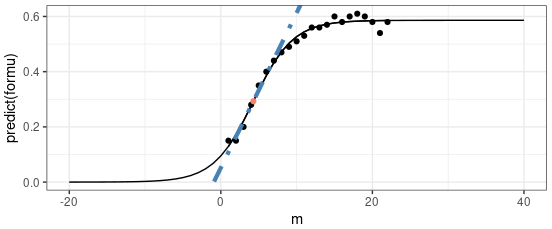
Here is an example of a neural network’s performance on a sine function. The neural network is trained to approximate the sine function but fails to do so for values in the gaps between -10 to -20 and 10 to 20. You can see that the model learns the region between -10 and 10 very well, but it simply overfits or “remembers” the training data. This example is very straightforward because we have only one dimension. So, this is probably the reason it can perform well on high-dimensional data: the network can build good connections across different dimensions. However, it is still limited to the existing patterns in the training set. The larger the network, the more patterns it can learn, but the less it can generalize.
|
Complexity of the Model: Capacity vs. Generalization

As shown in the example above, when we reduce the number of hidden layers and nodes, the model is limited to only a portion of the data. The model’s capacity is restricted, and it can only “learn” or “memorize” part of the training data.
Multi-layer Neural Nets