Principles of Biochemistry 7 |Enzyme Kinetics| Class Notes |HarvardX

Reaction Velocity

$\beta-galactoside + H_ 2O \xrightarrow{\beta-galactosidase} Galactose + R-Group$

With the concentration of the reactants and product, we define the velocity of the reaction.

The velocity of the reaction is either:

• the amount of product that is formed per unit of time
• the amount of substrate that is consumed per unit of time.

Measure the velocity of beta-galactosidase

$\beta-galactosidase$ could convert the ONPG, a colorless compound, to Galactose and ONP, which is a yellow compound. It could be measured by the spectrophotometer.

$$
V = \frac{d[P]}{dt}
$$

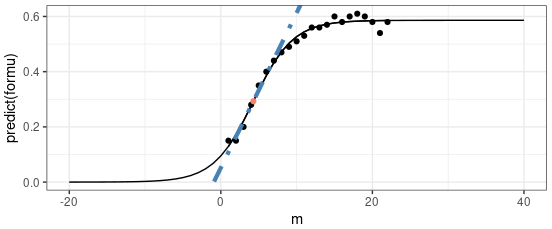
As we can see in the chart above, the velocity is changing over time since the substrate gets depleted.

But the first part of the reaction is almost linear which give us the way to define the velocity of the enzyme (Initial velocity)

V_mas: When the concentration of the enzyme was maintained, with the increase of the substrate’s concentration, the enzyme became the restriction factor. And so, it would not change its initial velocity and reach its max which is the feature of all enzymes.

Kinetic Model

$$
E + S \underset{k_ {-1}}{\overset{k_ 1}{\rightleftharpoons } } ES \underset{k_ {-2}}{\overset{k_ 2}{\rightleftharpoons } } P + E
$$

E: Enzyme
S: Substrate
P: Product

Since the concentration of the products was really low, the reverse reaction of $P + E \to ES$ is ignoble. The K_m was contributed by k₁, k_-1, and k₂.

• Formation of ES:
  • $V_ 1 = k_ 1[E][S]$
• Degradation of ES:
  • $V_ 2 = k_ {-1}[ES]+ k_ 2[ES]$
    $\ \ \ \ \ = [ES](k_ {-1} + k_ 2)$
• Steady state:
  • $V_ 1 = V_ 2$
    $k_ 1[E][S]=[ES](k_ {-1} + k_ 2)$

Michaelis and Menten constant

$$
\frac{[E][S]}{[ES]} = \frac{k_ {-1} + K_ 2}{k_ 1} = K_ m
$$

When the $[ES]$ is the rate-limited step:
High $K_ m$: low substrate affinity
Low $K_ m$: high substrate affinity

To calculate the free enzyme:
$[E_ T] = [E] + [ES]$
$[E] = [E_ T] - [ES]$
$K_ m = \frac{[E][S]}{[ES]}$
$\ \ \ \ \ \ = \frac{([E_ T]- [ES]) [S] }{ [ES]}$
$\ \ \ \ \ \ =(\frac{[E_ T]}{ES} -1)[S ]$

When the overdose of the substrate, all enzymes are combined with the substrate.
As a result, we can have:
$V_ 0 =k_ 2 [ES]$
$V_ {max} = k_ 2 [E_ T]$
$\frac{V_ {max}}{V_ 0} = \frac{K_ 2 [E_ t]}{K_ 2 [ES]} = \frac{[E_ T]}{[ES]}$

Under these circumstance ($[E_ T] = [ES]$), we can have:
$K_ m = (\frac{V_ {max}}{V_ 0} -1)[S]$
$V_ 0 = \frac{V_ {max}[S]}{K_ m + [S]}$

At the beginning of the chart above, the velocity of the Substrates is very low, too low to ignoble. Under these conditions, we can have:
$V_ 0 = \frac{V_ {max}[S]}{K_ m}$

When we have a very high concentration of Substrates, the $V_ 0$ is really high and theoretically equals the $V_ {max}$. As a result, we can have:
$V_ 0 = \frac{V_ {max}[S]}{[S]}= V_ {max}$

When the Concentration of the Substrate is equal to $K_ m$:
$V_ 0 = \frac{V_ {max}[S]}{K_ m + [S]}$
$V_ 0 = \frac{V_ {max}[S]}{2[S]} = \frac{V_ {max}}{2}$

Linearly the Michaelis and Menten equation

$V_ 0 = \frac{V_ {max}[S]}{K_ m + [S]}$
$\frac{1}{V_ 0} = \frac{K_m + [S]}{V_ {max}[S]}$
$\frac{1}{V_ 0} = \frac{K_m}{V_ {max}[S]} + \frac{[S] }{V_ {max}[S]}$

Then, we have Lineweaver-Burk:
$\frac{1}{V_ 0} = (\frac{K_m}{V_ {max}})(\frac{1}{[S]}) + \frac{1}{V_ {max}}$

$ y = mx+b$
$m$: $\frac{k_ m}{V_ {max}}$
$b$: $\frac{1}{V_ {max}}$

As you can see, when:
$0 = [S]$
Then:
$0 = (\frac{K_m}{V_ {max}})(\frac{1}{[S]})$
$\frac{1}{V_ 0} = \frac{1}{V_ {max}}$

When in the intercept with X axis:
$\frac{1}{V_ 0} = (\frac{K_ m}{V_ {max}})(\frac{1}{[S]}) + \frac{1}{V_ {max}}$
$0 = (\frac{K_ m}{V_ {max}})(\frac{1}{[S]}) + \frac{1}{V_ {max}}$
$\frac{K_ m}{V_ {max}[S]} = \frac{-1}{V_ {max}}$
$\frac{K_ m}{[S]} = -1$
$\frac{1}{[S]} = \frac{-1}{K_ m}$

Inhibitors

PDF slide: HarvardX

Competitive Inhibitor

Bind to the active site of the enzyme to prohibit the reaction
[ES] [EI] was formed and so we can make a prediction

• With the adding of the inhibitor, the affinity of the enzyme to the substrate was decreased, which suggest a $K_ m$ was increased.
• When substrate is higher, the $V_ {max}$ remain unchanged.
  Because the concentration of the inhibitor is constant, the substrate will out-compete the inhibitor. There for, the enzyme will reach the max velocity.

Similarly, we can have the function:
$$
EI \underset{k’_ {1}}{\overset{k’_ {-1}}{\rightleftharpoons } } E + S \underset{k_ {-1}}{\overset{k_ 1}{\rightleftharpoons } } ES \underset{k_ {-2}}{\overset{k_ 2}{\rightleftharpoons } } P + E
$$

$ \frac{[E][I]}{[EI]} = \frac{k’_ {-1}}{k’_ 1} = K_ I$
$ \frac{K_ m}{K_ I} = \frac{[E][S]}{[ES]} \times \frac{[EI]}{[E][I]}$
$ \frac{K_ m}{K_ I}(\frac{[I]}{[S]})= \frac{[EI]}{[ES]} $
$ \because [E_ T] = [E] + [ES] + [EI]$
$ \therefore \frac{K_ m}{K_ I}(\frac{[I]}{[S]})= \frac{[E_ T] - [ES] - [E]}{[ES]} $
$ \therefore \frac{K_ m}{K_ I}(\frac{[I]}{[S]})= \frac{[E_ T]}{[ES]} - 1 - \frac{[E_]}{[ES]} $
$ \because V_ 0 = k2[ES]; V_ max= K_ 2 [E_ T]$
$ \therefore \frac{V_ {max}}{V_ 0} = \frac{[E_ T]}{[ES]}$
$ \because K_ m = \frac{[E][S]}{[ES]}$
$ \therefore \frac{K_ m}{[S]} = \frac{[E]}{[ES]}$
$ \therefore \frac{K_ m}{K_ I}(\frac{[I]}{[S]})= \frac{V_ max}{V_ 0} - 1 - \frac{K_ m}{[S]}$

Now, we can have the special points on chart:

$\frac{V_ {max}}{V_ 0} = 1 + \frac{K_ m }{[S]} + \frac{K_ m}{K_ I}(\frac{[I]}{[S]})$
$\frac{V_ {max}}{V_ 0} = K_ m (1+\frac{[I]}{K_ I})\frac{1}{[S]} + 1$
$\frac{1}{V_ 0} = \frac{K_ m}{V_ {max}} (1+\frac{[I]}{K_ I})\frac{1}{[S]} + \frac{1}{V_ {max}}$

So, Compared the function which has no inhibitor, the Lineweaver-Burk equation:
$\frac{1}{V_ 0} = (\frac{K_m}{V_ {max}})(\frac{1}{[S]}) + \frac{1}{V_ {max}}$
We can find that they are similar.

Let’s say:
$\alpha = 1+\frac{[I]}{K_ I}$
$\therefore \frac{1}{V_ 0} = \frac{\alpha K_ m}{V_ {max}} \frac{1}{[S]} + \frac{1}{V_ {max}}$

Compared to the linear equationL
$y = mx + b$
the slope $m = \frac{\alpha K_ m}{V_ {max}}$

$\alpha K_ m = K_ {m, app}$
$K_ {m, app} > K_ m $

$K_ {m, app}$, apparent $K_ m$

Uncompetitive Inhibitor

They bind the enzyme only if they enzyme associated with substrate.
$E + S \rightleftharpoons ES +I \rightleftharpoons ESI $

1. $ E + S \underset{k_ {-1}}{\overset{k_ 1}{\rightleftharpoons } } ES \underset{k_ {-2}}{\overset{k_ 2}{\rightleftharpoons } } P + E$
2. $ESI \underset{k’_ {1}}{\overset{k’_ {-1}}{\rightleftharpoons } } ES + I$

In this situation, with the increased of the $[S]$, the $[ES]$ and $[P]$ was increased. But the $[ESI]$ was increased, too. As a result, some of the enzyme will be trapped into a nonproductive complex and the $V_ {max}$ would be reduced.

$\frac{1}{V_ 0} = \frac{K_ m }{V_ {max}}\frac{1}{[S]} + \frac{\alpha’}{V_ {max}}$
$\alpha’ = 1 + \frac{[I]}{K;_ I}$

As a result, the slope of the Uncompetitive inhibition function and the noninhibitor function are is the same

Mixed Inhibitor

The inhibitor which can bind the activity site of the enzyme and the enzyme substrate complex to inhibitor the productivity.

1. $EI \underset{k’_ {1}}{\overset{k’_ {-1}}{\rightleftharpoons } } E + S \underset{k_ {-1}}{\overset{k_ 1}{\rightleftharpoons } } ES \underset{k_ {-2}}{\overset{k_ 2}{\rightleftharpoons } } P + E$
2. $S + EI \underset{k’‘_ {1}}{\overset{k’‘_ {-1}}{\rightleftharpoons } } ESI \underset{k’_ {1}}{\overset{k’_ {-1}}{\rightleftharpoons } } ES + I$

In this case, $K_ m$ could increase, decrease, or stay the same which depend on the relative rate of the formation of the enzyme-inhibitor complex and the formation of the ESI complex.

In Lineweaver-Burk linear function:
$\frac{1}{V_ 0} = \frac{\alpha K_ m}{V_ {max}}\frac{1}{[S]} + \frac{\alpha’}{V_max}$
$\alpha = 1 + \frac{[I]}{K_ I}$; Effect of EI formation
$\alpha’ = 1 + \frac{[I]}{K’_ I}$; Effect of ESI formation

Case 1:
Inhibitor facors $E$ over $ES$:
$ K_ I$ dominates over $K’ _ I$
$\therefore K_ m$ increases
$K_ {m, app} = \frac{\alpha K_ m}{\alpha’}$

Noncompetitive Inhibitor:
$\alpha = \alpha’$
$K_ {m, app} = \frac{\alpha K_ m}{\alpha’}$
$K_ {m, app} = K_ m$

	y-intercept-1	x-intercept-1
Inhibitor	$V_ {max, app}$	$K_ {m, app}$
Absent	$V_ {max}$	$K_ m$
Competitive	$V_ {max}$	$\alpha K_ m$
Uncompetitive	$\frac {V_ {max}}{\alpha’}$	$\frac{K_ m}{\alpha’}$
Mixed	$\frac{V_ {max}}{\alpha’}$	$\frac{\alpha K_ m }{\alpha’}$