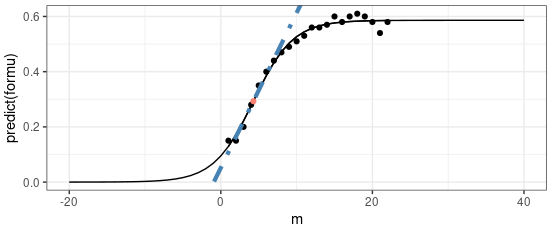
PCA

Example Dataset
Suppose we have the following dataset with 3 data points and 2 features ($x_1$, $x_2$):

$$
X =
\begin{bmatrix}
2.5 & 2.4 \\
0.5 & 0.7 \\
2.2 & 2.9
\end{bmatrix}
$$

X = np.array([[2.5, 2.4], [0.5, 0.7], [2.2, 2.9]])

Step 1: Center the Data

First, subtract the mean of each feature from the dataset to center it:

1. Compute the means:

   • Mean of $x_1$: $\text{mean}(x_1) = \frac{2.5 + 0.5 + 2.2}{3} = 1.73$
   • Mean of $x_2$: $\text{mean}(x_2) = \frac{2.4 + 0.7 + 2.9}{3} = 2.0$

2. Subtract the means:
   $$
   X_{ \text{centered} } =
   \begin{bmatrix}
   2.5 - 1.73 & 2.4 - 2.0 \\
   0.5 - 1.73 & 0.7 - 2.0 \\
   2.2 - 1.73 & 2.9 - 2.0
   \end{bmatrix} =
   \begin{bmatrix}
   0.77 & 0.4 \\
   -1.23 & -1.3 \\
   0.47 & 0.9
   \end{bmatrix}
   $$

X_centered = X - X.mean(axis = 0)

Step 2: Compute the Covariance Matrix

The covariance matrix shows how the features are related. Calculate it as:
$$
\text{Cov}(X) = \frac{1}{n-1} X_{\text{centered}}^\top X_{\text{centered}}
$$

1. Compute $X_{\text{centered}}^\top X_{\text{centered}}$:
   $$
   X_{\text{centered}}^\top X_{\text{centered}} =
   \begin{bmatrix}
   0.77 & -1.23 & 0.47 \\
   0.4 & -1.3 & 0.9
   \end{bmatrix}
   \begin{bmatrix}
   0.77 & 0.4 \\
   -1.23 & -1.3 \\
   0.47 & 0.9
   \end{bmatrix} =
   \begin{bmatrix}
   2.32 & 2.33 \\
   2.33 & 2.66
   \end{bmatrix}
   $$

2. Divide by $n-1 = 2$ (since $n=3$):
   $$
   \text{Cov}(X) =
   \begin{bmatrix}
   1.163 & 1.165 \\
   1.165 & 1.33
   \end{bmatrix}
   $$

# based on the equation
n = 3
CovX = X_centered.T@X_centered /(n-1)
# using function from numpy
np.cov(X.T)

array([[1.16333333, 1.165     ],
       [1.165     , 1.33      ]])

Step 3: Eigenvalues and Eigenvectors

Find the eigenvalues ($\lambda$) and eigenvectors ($u$) of the covariance matrix.

1. Solve $\text{det}(\text{Cov}(X) - \lambda I) = 0$ for $\lambda$:
   $$
   \text{det}
   \begin{bmatrix}
   1.163 - \lambda & 1.165 \\
   1.165 & 1.33 - \lambda
   \end{bmatrix}
   = 0
   $$
   This results in eigenvalues:
   $$
   \lambda_1 = 2.41, \quad \lambda_2 = 0.08
   $$

def Lambda(a,b,c):
    lambda1 = (-b+np.sqrt(b**2 - 4*a*c))/2/a
    lambda2 = (-b-np.sqrt(b**2 - 4*a*c))/2/a
    return lambda1, lambda2

a = 1
b = -(CovX[0,0] + CovX[1,1]) 
c = CovX[0,0]*CovX[1,1] - CovX[0,1]*CovX[1,0]

lm = Lambda(a,b,c)

(2.414643312171381, 0.07869002116195278)

2. Find eigenvectors ($u$):
   Solve $(\text{Cov}(X) - \lambda I)u = 0$ for each $\lambda$. The eigenvectors are:
   $$
   u_1 = \begin{bmatrix} 8.48 \\ -9.11 \end{bmatrix}, \quad
   $$

tmp1 = CovX - lm[0]* np.eye(CovX.shape[0])
xx = tmp.sum()
x2 = xx[0]/xx[1]
Length = np.sqrt(xx[0]**2+xx[1]**2)
x1 = 1/Length
x2 /=Length * -1

u = np.array([x1, x2])
print(u)

array([ 8.47987336, 9.10811172])

3. Variance of this component

$$
Variance = \frac{max(\lambda _1, \lambda _2)}{\lambda _1+\lambda _2}
$$

max(lm)/sum(lm)

0.9684

Step 4: Project Data onto Principal Components

Use the top eigenvector ($u_1$) to project the data into 1D (reduce dimensionality):

$$
X_{\text{projected}} = X_{\text{centered}} \cdot u_1
$$

1. Compute the projection:
   $$
   X_{\text{projected}} =
   \begin{bmatrix}
   0.77 & 0.4 \\
   -1.23 & -1.3 \\
   0.47 & 0.9
   \end{bmatrix}
   \begin{bmatrix}
   8.48 \\
   -9.11
   \end{bmatrix} =
   \begin{bmatrix}
   10.14 \\
   -22.30 \\
   12.15
   \end{bmatrix}
   $$

X_centered*u

array([ 10.14448093, -22.29905572,  12.15457479])

Final Results:

1. Principal Components:

   • The first principal component explains most of the variance ($97%$).

2. Transformed Data:

   • The dataset in 1D space:
     $$
     X_{\text{projected}} = \begin{bmatrix} 10.14 \\ -22.30 \\ 12.15 \end{bmatrix}
     $$

---

How to calculate Eigenvalues

Step 3.1: Find Eigenvalues

Eigenvalues are the roots of the characteristic equation:
$$
\text{det}(\text{Cov}(X) - \lambda I) = 0
$$

$$
\text{Cov}(X) =
\begin{bmatrix}
2.01 & 1.91 \\
1.91 & 2.03
\end{bmatrix}
$$

1. Subtract $\lambda I$ from $\text{Cov}(X)$:
   $$
   \text{Cov}(X) - \lambda I =
   \begin{bmatrix}
   2.01 - \lambda & 1.91 \\
   1.91 & 2.03 - \lambda
   \end{bmatrix}
   $$

2. Compute the determinant of this matrix:
   $$
   \text{det}(\text{Cov}(X) - \lambda I) = (2.01 - \lambda)(2.03 - \lambda) - (1.91)^2
   $$

3. Expand the determinant:
   $$
   \text{det}(\text{Cov}(X) - \lambda I) = (2.01)(2.03) - (2.01)\lambda - (2.03)\lambda + \lambda^2 - 1.91^2
   $$
   $$
   = \lambda^2 - (2.01 + 2.03)\lambda + (2.01 \cdot 2.03 - 1.91^2)
   $$

4. Simplify:
   $$
   \lambda^2 - 4.04\lambda + (4.0803 - 3.6481) = 0
   $$
   $$
   \lambda^2 - 4.04\lambda + 0.4322 = 0
   $$

5. Solve this quadratic equation using the quadratic formula:
   $$
   \lambda = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
   $$
   Here:

• $a = 1$, $b = -4.04$, $c = 0.4322$

$$
\lambda = \frac{-(-4.04) \pm \sqrt{(-4.04)^2 - 4(1)(0.4322)}}{2(1)}
$$
$$
\lambda = \frac{4.04 \pm \sqrt{16.3216 - 1.7288}}{2}
$$
$$
\lambda = \frac{4.04 \pm \sqrt{14.5928}}{2}
$$
$$
\lambda = \frac{4.04 \pm 3.82}{2}
$$

6. Compute the two eigenvalues:
   $$
   \lambda_1 = \frac{4.04 + 3.82}{2} = 3.96, \quad \lambda_2 = \frac{4.04 - 3.82}{2} = 0.08
   $$

Step 3.2: Find Eigenvectors

For each eigenvalue $\lambda$, solve $(\text{Cov}(X) - \lambda I)u = 0$.

For $\lambda_1 = 3.96$:

1. Substitute $\lambda_1$ into $\text{Cov}(X) - \lambda I$:
   $$
   \text{Cov}(X) - 3.96 I =
   \begin{bmatrix}
   2.01 - 3.96 & 1.91 \\
   1.91 & 2.03 - 3.96
   \end{bmatrix}
   =
   \begin{bmatrix}
   -1.95 & 1.91 \\
   1.91 & -1.93
   \end{bmatrix}
   $$

2. Solve the equation:
   $$
   \begin{bmatrix}
   -1.95 & 1.91 \\
   1.91 & -1.93
   \end{bmatrix}
   \begin{bmatrix}
   x_1 \\
   x_2
   \end{bmatrix}
   = 0
   $$

This expands to two equations:
$$
-1.95x_1 + 1.91x_2 = 0
$$
$$
1.91x_1 - 1.93x_2 = 0
$$

3. Simplify:
   $$
   x_2 = \frac{1.95}{1.91}x_1 \quad \text{(from the first equation)}
   $$

4. Normalize the vector (scale so that the length is 1):
   $$
   u_1 = \begin{bmatrix}
   0.71 \\
   0.71
   \end{bmatrix}
   $$

For $\lambda_2 = 0.08$:

1. Substitute $\lambda_2$ into $\text{Cov}(X) - \lambda I$:
   $$
   \text{Cov}(X) - 0.08 I =
   \begin{bmatrix}
   2.01 - 0.08 & 1.91 \\
   1.91 & 2.03 - 0.08
   \end{bmatrix}
   =
   \begin{bmatrix}
   1.93 & 1.91 \\
   1.91 & 1.95
   \end{bmatrix}
   $$

2. Solve the equation:
   $$
   1.93x_1 + 1.91x_2 = 0
   $$
   $$
   1.91x_1 + 1.95x_2 = 0
   $$

3. Simplify:
   $$
   x_2 = -\frac{1.93}{1.91}x_1
   $$

4. Normalize the vector:
   $$
   u_2 = \begin{bmatrix}
   -0.71 \\
   0.71
   \end{bmatrix}
   $$

Final Result:

• Eigenvalues:
  $$
  \lambda_1 = 3.96, \quad \lambda_2 = 0.08
  $$
• Eigenvectors:
  $$
  u_1 = \begin{bmatrix} 0.71 \\ 0.71 \end{bmatrix}, \quad
  u_2 = \begin{bmatrix} -0.71 \\ 0.71 \end{bmatrix}
  $$