Backpropagation Hand by Hand
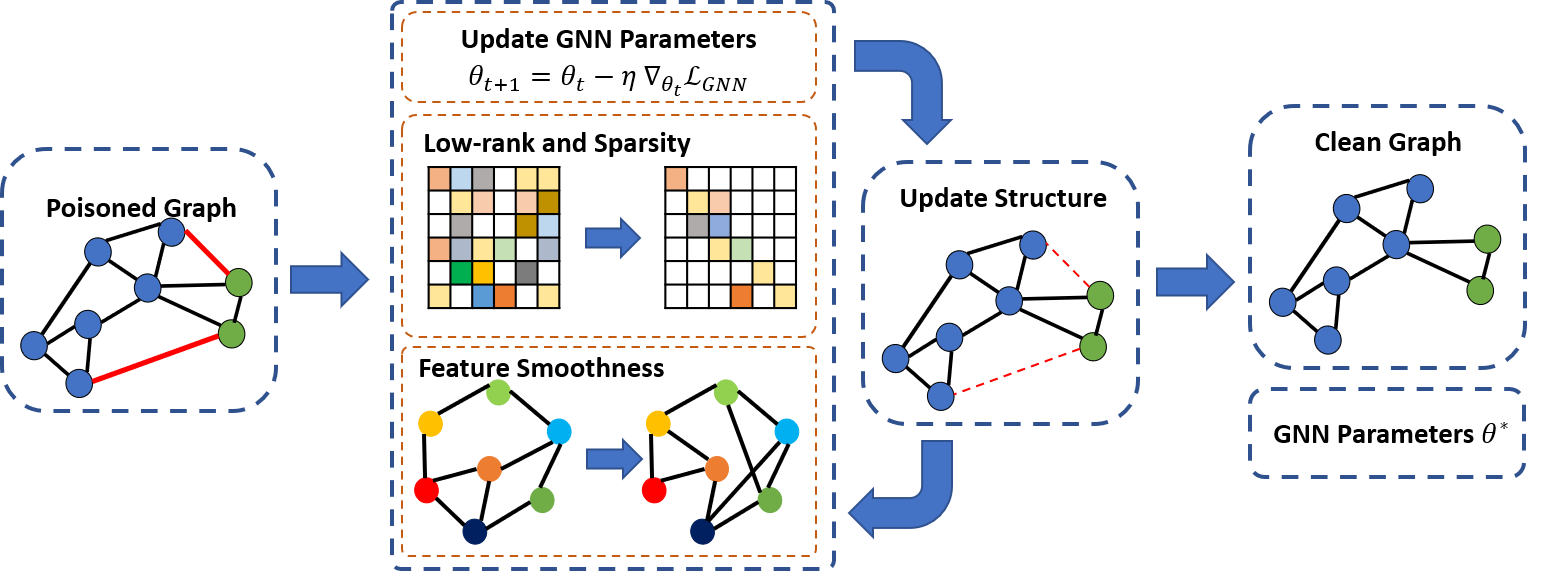
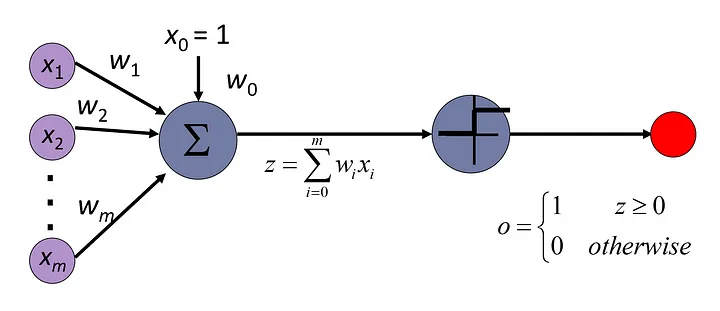
Backpropagation is the algorithm that trains neural networks by adjusting their weights to minimize the loss. It works by applying the chain rule of calculus to efficiently compute how the loss changes with respect to each weight. Starting from the output layer, it propagates the error backward through the network, layer by layer, updating the weights based on their contribution to the error.$$W^\ell\!\leftarrow W^\ell - \eta\, (a^ {\ell-1}) ^\top \delta^\ell,\quad b^\ell\!\leftarrow b^\ell - \eta\,\sum\delta^\ell.$$
Read more