library(ggplot2)
Distent <- function(P1,P2){
R = sqrt((P1[1]-P2[1])^2 + (P1[2]-P2[2])^2)
return(R)
}
Trans <- function(P1,P2){
D_s = Distent(P1,P2)
P2=c(P1[1]+D_s,P1[2])
return(P2)
}
Cir_D <-function(P1,P2,D=c(0,0),r=1,Space=pi/7){
X = seq(P1[1],P2[1],by=Space)
Y = sqrt(r^2-(X-D[1])^2)+D[2]
S=data.frame(X,Y)
return(S)}
Connet <- function(P1,P2,Space=pi/7,theta=pi/2){
P3 = Trans(P1,P2)
D=(P1+P3)/2
d=sqrt((P1-P3)[1]^2 + (P1-P3)[2]^2)
r=(d/2)/sin(theta/2)
l=(d/2)/tan(theta/2)
Cen_x =D[1]
Cen_y = D[2]-l
D=c(Cen_x,Cen_y)
S=Cir_D(P1,P3,D,r,Space=Space)
if(P1[1] -P2[1] > 0){
S$Y = (-1)*S$Y
}
Sin=(P2-P1)[2]/sqrt(sum((P2-P1)^2))
Cos=(P2-P1)[1]/sqrt(sum((P2-P1)^2))
X = S$X*Cos-S$Y*Sin
Y = S$X*Sin+S$Y*Cos
Line = data.frame(X=X-(X[1]-P1[1]),Y=Y-(Y[1]-P1[2]))
return(Line)
}
P1 = c(0,0)
P2 = c(6,0)
Connet(P1,P2)
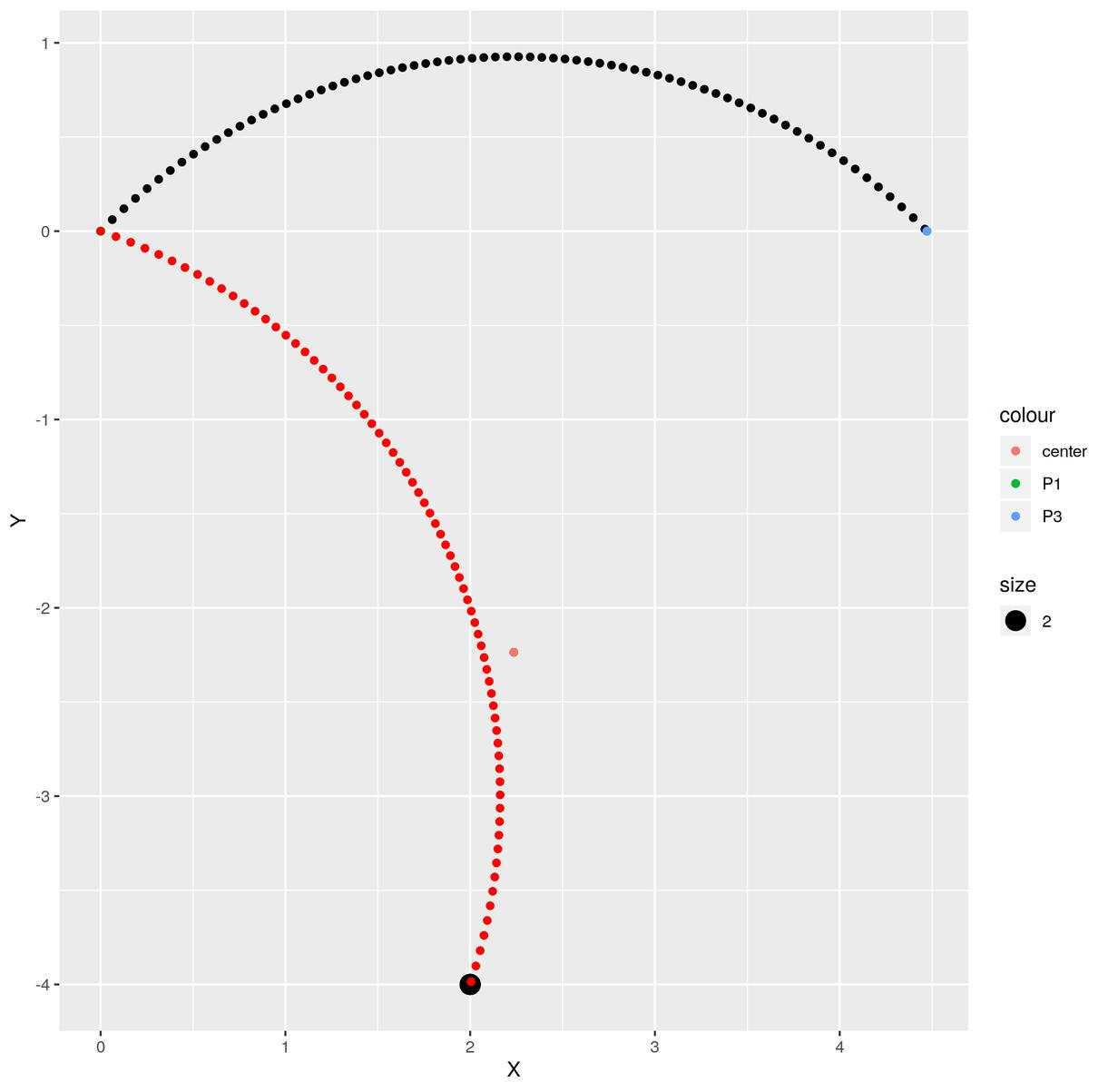
ggplot(Connet(P1,P2,pi/15),aes(X,Y))+geom_path()
|