python: geomitry calculation

Geomitry is fun

Area

Polygon

Draw a polygon

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

x = [0, 1, 2]
y = [0, 1, 0]

def PolyArea(x,y):
  # calculate the area of the polygon
  return 0.5*np.abs(np.dot(x,np.roll(y,1))-np.dot(y,np.roll(x,1)))

def sns_poly(x, y):
  # function for plot the polygon
  x = x +x[:1]
  y = y +y[:1]
  return [sns.lineplot(x=[x[i], x[i+1]], y=[y[i], y[i+1]])
    for i in range(len(x) -1)]


sns_poly(x, y)
plt.show()
PolyArea(x,y)

1.0

As we can see, the area of the polygon is 1

Example 2: More complicated polygon

x = [0, 0, 1, 2, 2]
y = [0, 2, 1, 2, 0]


PolyArea(x,y)
sns_poly(x, y)
plt.show()

3.0

Aear by shapely

library shapely could also calculate the areas of a giving polygon

# pip install shapely
from shapely.geometry import Polygon

# create a polygon by following order:
def creat_polygon(x, y):
  return Polygon([[i,j]for i,j in zip(x,y)])


x = [0, 0, 1, 2, 2]
y = [0, 2, 1, 2, 0]
P = creat_polygon(x, y)
print(P.area)

Circle

Reference:

• Plot the circle: Yann; 2012

Create a circle with scipy

import math
import matplotlib.pyplot as plt
from scipy.spatial.distance import euclidean

def Cir_arear(Center, P1):
  r = euclidean(Center, P1)
  area = math.pi * r * r
  #circumference = 2 * math.pi * r
  return area

# points for circle
Center = (0, 0)
P1 = (1,1)
radius = euclidean(Center, P1)
# points for intersect line
L1 = [-1.5, -1]
L2 = [0.5, 1.5]
Line = np.array([L1, L2])

fig, ax = plt.subplots(figsize = (5,5)) # note we must use plt.subplots, not plt.subplot
circle1 = plt.Circle(Center, radius, color='salmon', fill=False)
ax.add_patch(circle1)
ax.set(xlim=(-2,2), ylim=(-2,2),)
sns.lineplot(x=Line[:, 0], y = Line[:, 1])
plt.show()

from shapely.geometry import LineString
from shapely.geometry import Point


def Inters_CL(Center, P1, L1, L2, Plot=True):
  Line = np.array([L1, L2])
  radius = euclidean(Center, P1)
  Inter_vertics = []
  p = Point(Center).buffer(radius)
  l = LineString(Line)
  if p.intersects(l) == True:
    i = p.intersection(l)
    for index in range(len(i.boundary)):
      if i.boundary[index].coords[0] not in Line:
        Inter_vertics += [i.boundary[index].coords[0]]

  Inter_vertics = np.array(Inter_vertics)
  if Plot==True:
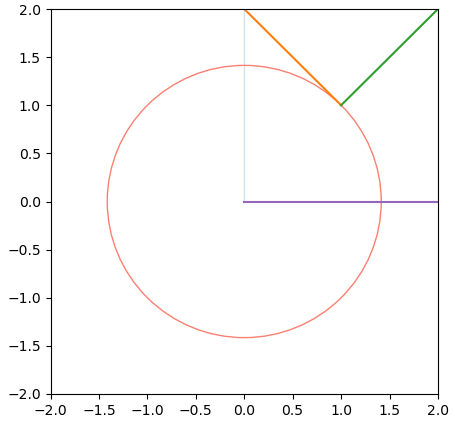
    circle1 = plt.Circle(Center, radius, color='salmon', fill=False)
    ax.add_patch(circle1)
    ax.set(xlim=(-2,2), ylim=(-2,2),)
    sns.lineplot(x=Line[:, 0], y = Line[:, 1])
    sns.scatterplot(x= Inter_vertics[:, 0], y = Inter_vertics[:, 1])
  return Inter_vertics

fig, ax = plt.subplots(figsize = (5,5)) # note we must use plt.subplots, not plt.subplot

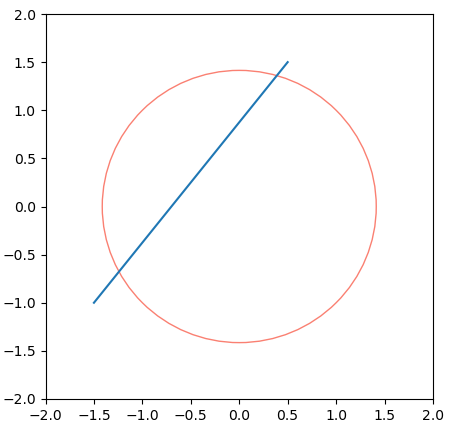
Inters_CL(Center, P1, L1, L2)
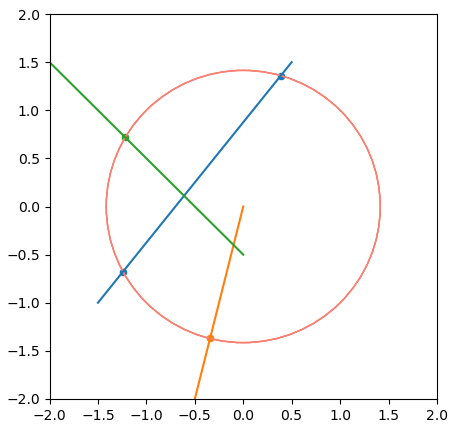
Inters_CL(Center, P1, [-0.5,-2], [0,0])
Inters_CL(Center, P1, [-2, 1.5], [0,-0.5])

intersect Area

x = [0, 0, 1, 2, 2]
y = [0, 2, 1, 2, 0]
P = Polygon([[i,j]for i,j in zip(x,y)])

# p is the circle defined above
Line = np.array([L1, L2])
radius = euclidean(Center, P1)
Inter_vertics = []
p = Point(Center).buffer(radius)

# intersection area of a circle and a polygon
p.intersection(P).area


fig, ax = plt.subplots(figsize = (5,5)) # note we must use plt.subplots, not plt.subplot
circle1 = plt.Circle(Center, radius, color='salmon', fill=False)
ax.add_patch(circle1)
ax.set(xlim=(-2,2), ylim=(-2,2),)
sns_poly(x, y)
plt.show()